みなさんこんにちは!今回は、「円運動」について紹介していきます。「円運動」とはその名の通り物体が円を描く運動ですが、この運動について把握する際に2通りの考え方があります。また、その考え方の内の1つで新しく「慣性力」の考え方について触れます。これらの考え方をマスターすれば、学生などは円運動の問題が解けるようになるでしょう。今回のページでは1つ目の考え方について紹介し、次回で2つ目の考え方について紹介していこうと思います。それでは行ってみましょう(^^)/
等速円運動の特徴
まずは「等速円運動」について紹介していきます。
「等速円運動」とは、「速さ(速度の大きさ)が一定の円運動で、速度の向きは時々刻々変化し、たえず円の接戦方向を向いている」という物です。もう少しだけかみ砕いて言うと、「物体の速さは一定で、直線ではなく円を描いて運動するので、物体の進行方向は常に変化している。また、その変化の方向は円の接線方向である」ということです。(※1)
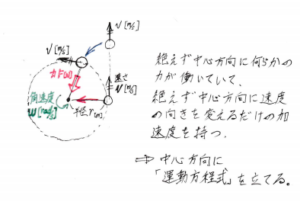
速度の向きが常時変化しているということは、たえず中心向きに何らかの力が働いている、すなわち、たえず中心向きに速度の向きを変えるだけの加速度があると考えられます。
ここで、運動している物体(=加速度を持つ物体)について考える時は、「運動方程式」を立てて考えるという話がありましたね。つまり、円運動について考える時も、回転の中心の方向に加速度を持っているので、その中心の方向に関する運動方程式を立てて考えていきます。これを、「円運動の運動方程式」などと言ったりします。
また、一度は物理の授業を受けたことがある人は「向心力」や「遠心力」という言葉を聞いた事があるかも知れません。しかし、「向心力」や「遠心力」の違いがイマイチわからなかったりしてこの言葉に惑わされる場合は、いったんこれらの言葉を忘れてしまいましょう!とにかく、「円運動では回転の中心方向に加速度を持つから、円運動の運動方程式を立てる」と覚えておけばOKです!そして、これが冒頭で話した1つ目の円運動の考え方になります。
※1【補足】ここで、上記では「速度」と「速さ」を区別したような書き方をしていますが、「速度」と「速さ」は少し違います。「速度」はベクトルで、「速さ」はスカラー量です。ベクトルというのは、「大きさ」と「向き」を示すものです。いわゆる矢印のようなものですね。スカラー量とは、「大きさ」のみを示した量です。つまり、「速さ」は「一秒あたりに進む距離(m)」のみを示しますが、「速度」は「一秒あたりに進む距離(m)」と「その向き」を示します。
円運動の運動方程式
ということで、今度は円運動の運動方程式について紹介していこうと思います。
早速ですが、円運動の運動方程式は次のような形をしています。

また、円運動の運動方程式は等速円運動では勿論、等速でない円運動でも使えます!(等速でない円運動=非等速円運動では、力学的エネルギー保存則と円運動の運動方程式を立てて解きます。)
ちなみに、円運動の運動方程式が何故この形をしているかについては、次の図の通りです。別に覚えておく必要はないので、興味がある人だけ見てみてください。
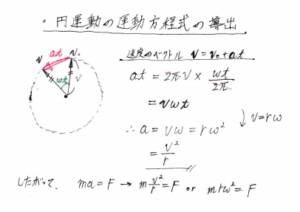
ここで、ωは角速度といい、単位は[rad/s]で表されます。
それでは、今回はここまでです。次回いよいよは2つ目の考え方について紹介していきます。それでは、おつかれさまでした!


コメント