皆さんこんにちは！
今回は「運動量と力積の関係」について紹介していきます。
「運動量」と「力積」の定義を抑えられた人なら、この両者になにか関係があるのは気づいているかもしれません。これから、「運動量」と「力積」に成り立つ具体的な関係について紹介していきます。また、最後には反発係数についても少し触れていきます！
運動量と力積の関係
前回の「運動量保存則」のところでは、複数の物体間で内力のみが働いて、外力が働かない時に運動量の和が保存される（一定に保たれる）という話をしました。これは、例えば2つの物体が衝突するとしたら、2つの物体の衝突前の運動量の和と衝突後の運動量の和が、外力の影響がない限り同じだということです。ここで、2つの物体全体では運動量の和は保存しますが、片方の物体のみの運動量に注目すると、衝突の前後でもう片方に力を及ぼされた分だけ運動量が変化する事になります。したがってこの場合は、各物体において運動量と力積の間に次のような関係が成り立ちます。
また、この2つの物体の運動量と力積の関係式を足すと見事に運動量保存則の式が成立していますね。これにより、「物体の運動量は力積によって変化するが、力のやり取りをする物体全体の運動量は保存される」ということが数学的にも示され（式でも示され）ました。
反発係数（eの文字を用いて表現されることが多い）
この項目の最後に、新しい概念「反発係数」について紹介しようと思います。
反発係数とは、「2つの物体の衝突における、衝突前の相対速度と衝突後の相対速度の比」といえます。
式にすると、次の通りです。
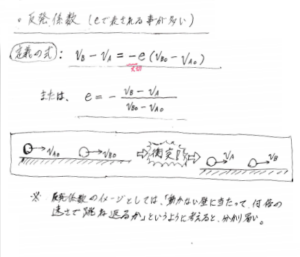
言葉だけではわかりづらいかも知れないので、実際の衝突のイメージを踏まえて考えてみましょう。
例えば、上の図の様に接近する2つの物体A,Bがあったとしましょう。そして、衝突前のAの速度をv、Bの速度をV、また、衝突後のAの速度をv’、Bの速度をV’になるとします。この時それぞれの相対速度は、衝突前は「V－v」、衝突後は「V’－v’」となりますね。したがって反発係数は、定義が「衝突の前後の相対速度の比」なので、「e=－(V’－v’)/( V－v)」となります。ちなみに、何故マイナスが付くかというと、反発係数は正の値にしかならない値と決まっているからです。例として今の式を再度見てみると、衝突前と後の速度の大小関係は「V’>v’」、「V＜v」ですよね。つまり、相対速度の比にマイナスをつけないと反発係数は負の値になってしまいます。ですから、「－」を付けることをわすれないようにしましょう！
もう一つ例をみてみましょう。先ほどの例は2つの物体が衝突の前後で同じ方向に運動していますが、今度は衝突の前後で逆方向に運動している例です。
今回も、衝突前のAの速度をv、Bの速度をV、また、衝突前のAの速度をv’、Bの速度をV’になるとしましょう。この時それぞれの相対速度は、衝突前は「V+v」、衝突後は「V’+v’」となりますね。したがって、反発係数は「e=( V’+v’)/( V+v)」となります。
ここで、「さっき言っていたeの定義とは全然ちがう形ジャン。『－』もついてないし。ワケワカンネ」とかいう声が聞こえてきそう(-_-;)ですが、問題ありません。これも先ほど紹介した式から導出できることを、これから説明していきます。
まず、図の方で最初に、物体の運動の方向について「正の方向」を設定しましたよね。つまり、この方向と逆方向に運動してる物体は「負の方向」に運動していることになるので、式にするとこの物体の速度の項には「－」がつきます。このことを踏まえて、反発係数の定義の式に代入してみましょう。
すると、「e=－｛V’―（−v’）｝/｛−V−v｝= ( V’+v’)/( V+v)」となり、うまくつじつまが合いましたね^^
（ちなみに、壁に物体がぶつかる時は、上の例のBの物体の速度を0とおくと計算できます）
以上より、反発係数は最初に紹介した定義で表されるわけです！
今回はここまでです！上記では「反発係数」が何かを紹介していきました。しかし、実はこの「反発係数」は一般的に3種類に分類されています。次回は、その「反発係数」の3種類の分類について解説していきます。それでは、おつかれさまでした！
コメント