皆さんこんにちは!「後編」では、「力の関係式」の続きを扱っていきます。
それでは、前回の続きです!
力の間の関係式(続)
物体が静止している時
次に、「物体が静止しているとはどういうことか」について解説していきます。
物体が静止しているとは、つまり、あらゆる方向において「物体に働く力が釣り合っている」ということです。
言い換えると、物体にある複数の方向からの力がかかっていた時に、それらの力が全て打ち消し合って、結局は物体にかかる力が0になっているという状態です。イメージし易いように、下の図を見てみましょう。
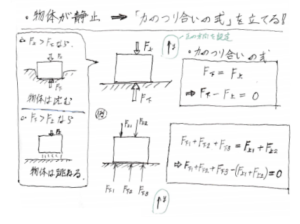
例えば、物体に垂直方向に対して上下から力がかかっているとします。この時、上にかかる力の合計と下にかかる力の合計が同じだとしたら、それぞれの力は互いに逆向きに働いているので、お互いを打ち消す事になります。すると、物体にかかる力の影響がなくなるので、運動をしないということになります。
(したがって、逆にどちらかの力が少しでも大きいとなると、物体はその力の方向に動いていってしまうわけです。)
では、このイメージを今度は式で捉えてみましょう。上側にかかる力の大きさF上と、下側にかかる力の大きさF下は等しいので、この2つの力の間には「F上 = F下」の関係が成り立ちますよね。つまり、この「F上 = F下」こそが「力のつり合いを示した式 ⇒ 力のつり合いの式」になります。
また、こう考える事もできます↓
まず、物体の運動を考えるときには、「正の方向」を決めてから考えるんでしたね。ということで、今回は垂直方向にしか力がないので、垂直方向についてのみ考えるとして、垂直上向きの方向を「正」としてみましょう。そうすると、この方向を力の式の符号に対応させるので、「正」の方向を向いている下側の力F下の符号は「+」、「正と逆 = 負」の方向を向いている上側の力F上の符号は「-」となります。したがって、これらの力の大きさの総和(合計)を考えてみると、「F下 - F上 = 0」となるわけです。つまり、これも「力のつり合いの式」となります。確かに、先程示した式「F上 = F下」の項を移項した形になっていますね(*´ω`)
つじつまが合います!
以上より、「力のつり合いの式」とは「F(正の方向に働く力の合計) - F(負の方向に働く力の合計) = 0」あるいは「F(正の方向に働く力の合計) = F(負の方向に働く力の合計)」の形になります(どちらを使ってもいいです!)。
まとめ
最後に、以上のことを踏まえて、物体に働く力の把握の仕方と、運動あるいは静止している物体を扱う時にどのような力の関係式を使うのかを、改めておさらいしていきましょう。
◎物体が得る5種類の力[()の中は単位]
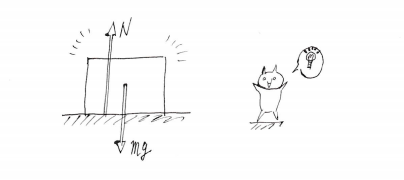
①重力 mg(N)
②垂直抗力 N(N)
③摩擦力 ・静止摩擦力 F(N)≦ µN(N) . ・動摩擦力 µ’N(N)
④糸の張力 T(N)
⑤バネの弾性力 kx(N)
重力あるか→垂直抗力あるか→摩擦力あるか→糸の張力あるか→バネの弾性力あるか」という様に、5つの力が物体に働いているのかを順に確認していく。
◎力の間の関係式
A:物体が静止(もしくは等速度運動)している時
⇒力のつり合いの式「F(正の方向に働く力の合計) = F(負の方向に働く力の合計)」などを立てる。
B:物体が運動している時
⇒運動方程式「ma=F」を立てる。
以上です。おつかれさまでした!
コメント