みなさんこんにちは!ここからは2回にわたって「運動の法則」を扱っていきます。【前編】では、主に「物体に働く5つの力」と「力の関係式」について紹介していきます!
物体の運動の状態を極端に二つに分けるとすれば、それは「動いている」か「動いていない」になります。ここで、物体が動いているにせよ、動いていないにせよ、物体には何かしらの力がかかっていたりします(例えば、重力など)。したがって、これらの物体にかかる力を把握することが、物体の運動について考えていく第1歩となります。
ということで、まずは理想的な空間における「物体に働く5つの力」をまず把握して、それから「物体が静止している時と動いている時の力の考え方」について学習していきましょう!
物体に働く5つの力
物体の運動(動いていても、静止していても)を考えていく際には、まずは物体に働く力を把握するところから始まります。そして、その物体に働く力というのは、理想化された空間においては、基本的に5種類存在すると言われています。たったの5種類です!それでは、その力について下にまとめてみます。

※問題によっては、浮力や空気抵抗なども出てきますが、基本的には物体が得る力は以上の5種類になります。
したがって、力学の問題を解く時とかに、物体に働いている力を確認していくとなったら、上の表の①から順に働いているか確認していきましょう。つまり、「重力あるか→垂直抗力あるか→摩擦力あるか→糸の張力あるか→バネの弾性力あるか」という様に、5つの力が物体に働いているのかを順に確認していきましょう!
力の間の関係式
それではいよいよ、「物体が静止している時と動いている時の力の考え方」について取得して行きましょう!
物体が動いている時
まず、「物体が動いている」とはどういうことかについて解説していきます。
早速ですが、物体が動いている時は、力と加速度と質量の間に次のような関係式が成り立ちます。
Ma=F
これを「運程方程式」と言います。つまり、運動している物体について考えていくときは、基本的にこの式を使って考えていきます。
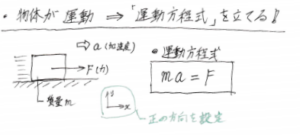
それでは、この運動方程式が何なのか、もう少し掘り下げてみましょう。
理想的な空間では、特に摩擦や物体を止める力などがない場合は、一度力を加えられると物体は動き続けるという話が前の記事でありましたね。つまり、物体が何かしらの力の影響を受けた時、物体は運動します。また、物体が運動する原因は力なので、力が働いている間は、物体には加速度が生じるという話もありました。
したがって、力と加速度の間には比例関係がなりたつと考えられます。
力F∝加速度a
そして、比例関係が成り立つという事は、力Fと加速度aの間には「F=〇×a」の(関係)式が成り立つという事ですね。ここで、力Fと加速度aの比例定数(=〇に入る定数)を質量mとおいてみましょう。
そうすると、式は「F=ma」の形になりますが、果たしてこの形が物理的にふさわしいかどうか考えてみましょう。
ここで、想像して見て下さい。例えば、止まっているmが大きい物体と小さい物体に同じ大きさの力Fを働かせたとしたら、大きい方は重いので、小さい方よりあまり加速できないですよね。一方で、小さいほうは大きい方より加速し易いですよね。
つまり、運動方程式「ma=F」は物理的につじつまが合った形をしているので、成り立つ事が納得いきますよね。
いかがでしたでしょうか。この先もまだこの単元で紹介する知識があるので、本日は一旦以上です。次回もまた「運動の法則」の続きを扱っていきます。それでは、お疲れさまでした!


コメント