皆さんこんにちは!前回の記事では「理想化された空間」と「速度と加速度」について扱いました。今回はその続きで「等加速度運動」と「放物運動」の基本的な考え方について紹介していきます。
それでは早速、行ってみましょう!
加速度運動の2つの解き方
ここで、物体の運動の一つである「等加速度運動」について学習しましょう。これは、この先理解するうえで大切な知識になるので、覚えておきましょう。
①等加速度運動の三つの式の利用
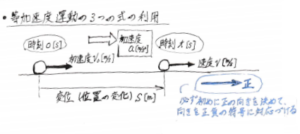

ちなみに、上の式で加速度の項aがa=0になった運動を「等速度運動」と言ったりします。
※また、物体の運動を扱う際には、まずはじめに「正の向き」という物をきめて、向きを式の正負の符号に対応づけて考えましょう。つまり、設定した「正の向き」を向いている力や速度の項には+(プラス)が付くし、逆に、「正の向きと逆向き」を向いている力や速度の項には-(マイナス)が付きます
②v-tグラフ(速度―時刻グラフ)の特徴の利用
A:グラフの傾き=加速度
B:グラフとt軸の囲む面積=変位(距離の変化量)
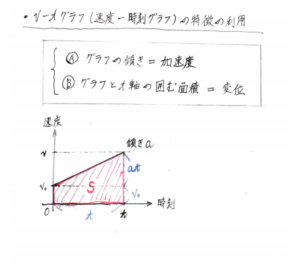
基本的に、等加速度運動をする物体の問題は以上の二つの知識を用いて解きます。
放物運動
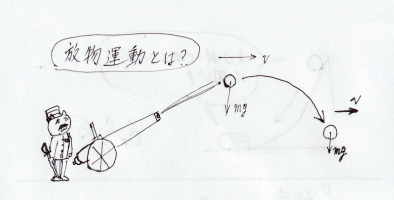
放物運動とは一見つかみどころのない運動に見えるかも知れませんが、実は、水平方向(x方向)と垂直方向(y方向)に分解して考えてみると単純な運動をしています。単純な運動とは具体的にどんな運動をしているのか…
それは、水平方向に「等速度運動」、垂直方向に「等加速度運動」です!
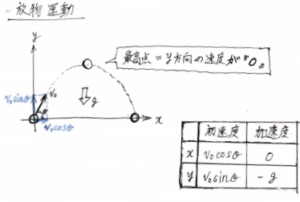
つまり、理想空間で発射された物体の速度を水平方向と垂直方向のそれぞれの方向で観察したら、この運動になっていたという訳です。(現実空間でも、勢いよく球を発射すればほぼこんな感じの運動をするはずです。)
※それでは、これからそうなる理由を説明いたしましょう。まず、これは物理で頻繁に使う大切な考え方なのですが(だからここで必ず覚えて下さい)、 任意の方向を向いている物体にかかる力や速度は、垂直方向と水平方向などの二つの方向に分解して考えることができます。(また、それぞれの分解した方向の力や速度というのは、三角関数を用いて求める事が出来ます。)
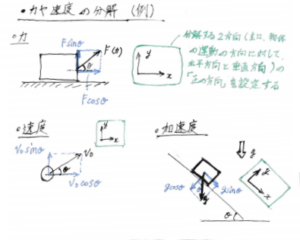
そして、発射した物体にかかる力をそれぞれの方向毎に考えると、水平方向にはなにもかかっていませんが、垂直方向には下向き(設定したy軸の負の向き)に重力がかかっているので、下向きに加速度が生じている事になります。
だから、水平方向は等速度運動となり、垂直方向は等加速度運動となります。
まとめ
いかがでしたでしょうか。それでは、今回の単元の内容を以下にまとめておきます。
・「速度」の定義は「単位時間(一秒)あたりに物体が進む距離(m)」
・「加速度」の定義は「単位時間(一秒)あたりの速度の変化量(m/s)」
・物体は、力が加わっている時に加速度が生じる。
・放物運動の正体は、水平方向に「等速度運動」、垂直方向に「等加速度運動」している。
・物体に任意の方向で働く力や速度は、二つの方向(主に水平方向と垂直方向)に分解できる。
(また、その分解した物の大きさは三角関数を用いて計算可能)
おつかれさまでした!それではまた。

コメント