今回は「運動量」と「力積」という量の考え方、「運動量保存則」について紹介していきます。急に「運動量」や「力積」と言われても何が何だかさっぱりと思うかもしれません(´・ω・`)
しかし、このページを読み進めていったらこれらが何なのかだんだんわかってくると思います(*´ω`)
ということで、さっそく始めていきましょう!
「運動量」とは
まず最初に紹介するのは、「運動量」です。運動量とはいったいどういう意味をもった量なんでしょうか?
運動量の物理的な意味は、「物体の運動の勢い」を表す量(物理量)です。
ここで、「物体の運動の勢い」についてイメージしてもらうために、一つ例を出してみましょう。例えば、重さが120kgある鉄球と重さが1kg程度しかないボールがあったとしましょう。ここで、鉄球とボールが同じ速度でぶつかってきたら、ボールは大丈夫だったとして重い鉄球の方には大きく跳ね飛ばされると思いますよね。一方で、いくら軽めのボールでも剛速球でぶつかってきたらかなり痛い思いをすると思います。つまり、このイメージのとおり、「物体の運動の勢い」というのは物体の「質量」と「速度」によって決まります。
したがって、運動量の定義は質量mと速度vの積で表される形をしています。
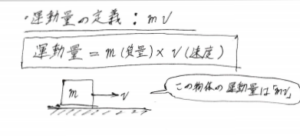
「力積」とは
次に「力積」について紹介していきます。「力積」とはどういう量かというと、「物体の運動量をどれだけ変化させたか」を表す量です。
ここで、先ほどの運動量の話を踏まえると、運動量を変化させるというのはすなわち、物体の運動の勢いを変化させるということになります。では、「物体の運動の勢いを変化させる」にはどうすれば良いのでしょうか?
その答えは、力を物体に加えてあげればいいんです(・∀・)
動いている物体に力を加えてあげれば、その勢いを強めも弱めもできますよね。単純な話です。
そして、力を加える時間が長いほど、また加える力の大きさが大きいほど物体の運動は変化させやすいですよね。
つまり、「力積」とは「物体の運動量をどれだけ変化させたか」を表す量なので、物体に加える力の大きさやその時間によって決まる量になるわけです。
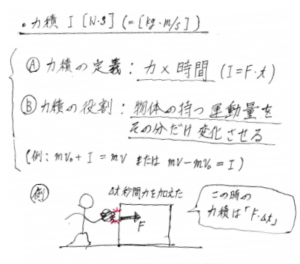
したがって、「力積」の定義は力Fと力を加える時間Δtの積で表される形になります。
運動量保存則
続いては、「運動量保存則」について紹介します。「運動量保存則」とは、「衝突・分裂・合体のように、考えている物体系(物体の集まり)において内力のみが働く(=外力が働かない)方向について運動量の和は変化せず一定である」というものです。
つまり、複数の物体があるとしたら、その物体間のみで力のやりとりがあり、それ以外の外の要素からの力(外力)の影響を受けない時に、その複数の物体の運動量の和は一定に保たれるということです。
したがって、運動量保存則の式は次のようになります。
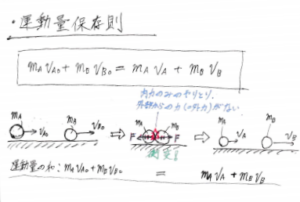
以上、「運動量」と「力積」、そして「運動量保存則」の紹介でした。次回はこの続きで、「運動量と力積の関係」について扱っていきます!
それでは、おつかれさまでした。


コメント